
70多门A-Level科目中,A-Level数学是比较容易拿高分的,但是涉及到的知识点也是十分庞杂,下面,跟随锦秋陈天然一起来看看有关于机械数学计算质心解题技巧。
今天就来带大家看看Mechanics中的重要考点,如何找均匀薄层物体的质心:masscenterofanuniformlamina。
我们首先来看规则形状的均匀分布的物体的质心。书上给出了3种规则形状的质心位置:长方形、三角形、扇形和圆形。
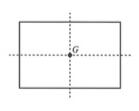
对于一个均匀分布的长方形,它的质心在长方形横竖两天对称轴的交点处,也是长方形两条对角线的交点。
若长方形的长为a,宽为b,且以左下角定点A为原点建立直角坐标系,则G的坐标为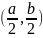 。
。
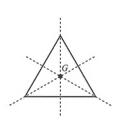
对于一个均匀分布的三角形,它的质心在三角形三边中线的交点处。若将三角形放置在平面直角坐标内,三角形三个顶点坐标分别是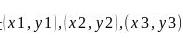 ,则质心坐标为
,则质心坐标为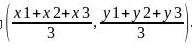 。
。
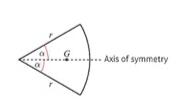
对于一个均匀分布的扇形,它的质心在扇形的对称轴上。若扇形面积为r,圆心角为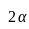 ,则质心和圆心之间的距离为。
,则质心和圆心之间的距离为。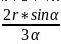 。
。
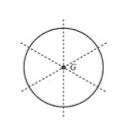
最后,也是最简单的,对于一个均匀分布的圆,质心就是圆心。
这个时候有同学就会问了,这些规则图形我都会背公式,但是考试里有很多不规则的图形,那不规则的图形该怎么计算它的质心呢?对于这一类题目,我们将我们不熟悉的不规则图形,通过分割或者补全的方式,转化为多个我们熟悉的规则图形的组合,先寻找规则图形的质心,再把每一个规则图形看作是一个质点(particle),通过寻找多个质点的质心的方式,来找到不规则图形的质心。
那么,首先我们来复习一下多个质点的质心该如何寻找。我们先构造一个平面直角坐标系,在直角坐标系内,确定每一个质点的坐标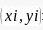 和每一个质点的质量
和每一个质点的质量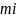 ,则整体质心的横纵坐标为
,则整体质心的横纵坐标为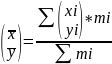 。
。
如果运用分割法,假设我们将原图形分割成n个规则图形,并放入直角坐标系内,每个规则图形的质点为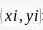 ,每一个规则图形的质量为
,每一个规则图形的质量为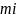 ,则原图形质心的横纵坐标为
,则原图形质心的横纵坐标为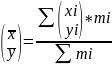 。
。
如果运用补全法,假设我们通过补全n个规则图形将原图形补充成一个大的规则图形,并放入直角坐标系中,大的规则图形的坐标为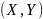 ,质量为
,质量为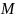 ,每个被补充上去的规则图形的质点为
,每个被补充上去的规则图形的质点为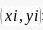 ,每一个规则图形的质量为
,每一个规则图形的质量为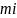 ,则原图形质心的横纵坐标为
,则原图形质心的横纵坐标为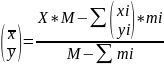 。
。
无论是用分割还是补全,规则图形的质量用面积乘以单位面积质量来计算,即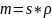 。
。
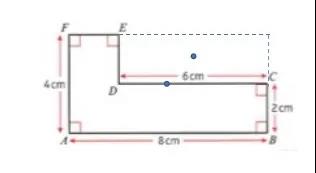
下面我们来通过一道例题来看看怎么运用上面的方法来找到不规则图形的质心。如图是一个均匀分布的不规则形状薄片,我们将运用两种方法来找到质心的位置。
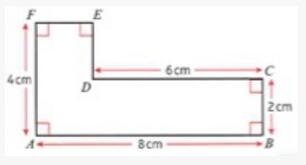
首先我们使用分割法,将这个不规则图形分割成两个规则的长方形:
以A为原点,则左边的长方形的质心为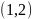 ,右边的长方形质心为
,右边的长方形质心为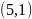 ,左边长方形的质量为
,左边长方形的质量为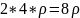 ,右边长方形的质量为
,右边长方形的质量为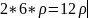 。则原图形的质心为:
。则原图形的质心为: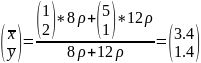 。
。
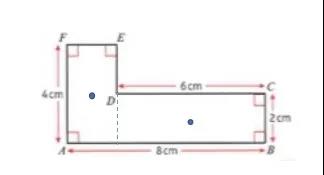
然后我们来使用补全法,通过补全右上方的小长方形,将这个不规则图形补成一个大的长方形。
补全后的大长方形质心坐标为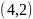 ,补充的小长方形坐标为
,补充的小长方形坐标为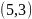 ,大长方形的质量为
,大长方形的质量为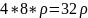 ,小长方形的质量为
,小长方形的质量为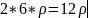 。则原图形的质心为:
。则原图形的质心为: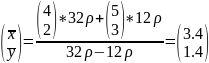 。
。
当然这一类题目在考试里还会有各种变化,例如不同部位的密度不同,巧妙分割可以减少计算等,这些都要靠同学们在课后多多练习,以不变的规则和公式对应各种变化。
更多有关A-Level科目及考试等方面的信息,大家也可以扫码关注锦秋A-Level进行了解,锦秋A-Level紧抓中国学生理科优势,进行课程组合化。开设数学、物理、化学、生物、经济学、会计学等课程,帮助学生以优异成绩申请更好的大学。

| 大学名称 | QS排名 |
|---|---|
| 麻省理工学院 | 1 |
| 剑桥大学 | 3 |
| 斯坦福大学 | 3 |
| 牛津大学 | 2 |
| 哈佛大学 | 5 |
| 加州理工学院 | 6 |
| 帝国理工学院 | 7 |
| 伦敦大学学院 | 8 |
| 苏黎世联邦理工大学 | 8 |
| 芝加哥大学 | 10 |
| 新加坡国立大学 | 11 |
| 宾夕法尼亚大学 | 13 |
| 洛桑联邦理工学院 | 14 |
网络优惠
预约试听
A-Level
雅思
留学咨询
留学规划