A-Level数学：分类探讨Statistics三大分布间的近似条件

A-Level进阶数学Statistics中的一个重要知识点：二项分布、正态分布、泊松分布。今天，范倩倩讲师将从以下三个方面分别去讨论和研究三大分布间的近似条件。

1. Using the Poisson distribution to approximate the binomial distribution 我们无论在做课后练习或是真题试卷时，经常会遇到n很大的题型，这种情况下直接求二项分布的概率是相当困难的，学会使用泊松近似是比较简单有效的方法。

那么二项分布需要满足什么条件可以使用泊松近似呢？

就是需要重点记忆的两个条件啦！！

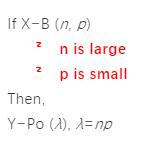
需要注意的是这里并没有明确的规则来定义“large n”和“small p”，但通常np≤10就满足要求。一般来说，n的值越大，p的值越小，近似就越准确。因为在这种情况下，(1-p)将接近1，因此Var(X) =np(1-p)将接近分布的均值，即E(X) =np。这满足了泊松分布模型中均值和方差接近的条件。

2. Using the normal distribution to approximate the binomial distribution

当n很大时，对于二项分布概率还可以使用正态近似求解，但是只有p接近0.5时近似才成立, 因为正态分布是对称的。

这里有个小陷阱是：二项分布是离散分布，而正态分布是连续的。

如果我们使用的是一个二项分布的正态近似值，就需要在计算概率时应用连续性校正。

例：

P(X＞5)≈P(Y＞5.5)

P(X=9)≈P(8.5＜Y＜9.5)

P(X≤3)≈P(Y＜3.5)

3. Using the normal distribution to approximate the Poisson distribution

如果泊松分布的平均值很大，那么我们可以使用正态近似。选择正态分布，是因为可以使其具有与原泊松分布相同的均值和与原泊松分布相同的方差。

同样地，在这里“large λ”又如何来判定呢，在泊松分布中我们认为当λ＞10就可以认定为“large”。

敲重点！！

对于二项分布，有两个可能的近似，取决于p是否接近0.5 (在这种情况下，使用正态分布)或者p很小 (在这种情况下，使用泊松分布)。如果你不确定使用哪种近似，这里提供一个有用的小技巧：计算均值np。如果np≤10，选择泊松近似。如果np＞10，那么选择正态近似。

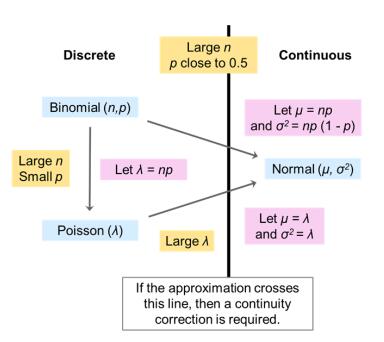
除此之外，同学们也可以利用这个下图来辅助记忆三个近似之间的条件哦~~~

更多有关A-Level科目及考试等方面的信息，大家可以扫码关注锦秋A-Level进行了解！