
在A-level所有科目中,A-level数学是比较难的一个科目,A-level数学有很多解题技巧和方法,今天,锦秋小编将要为大家介绍的是分部积分法,针对该方法的重点、难点等方面进行详细解答,希望对大家有所帮助。
关于分部积分法的技巧或者说学生经常疑惑的地方就是两个:
学生都知道使用公式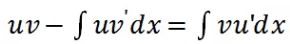 , 但是具体应用时, 总是不知道选谁当U选谁当V,即使最后试验出来U与V也太耗时了,也就是说:同学们想找个简易的判断谁当U,谁当V的办法是比较困难的。
, 但是具体应用时, 总是不知道选谁当U选谁当V,即使最后试验出来U与V也太耗时了,也就是说:同学们想找个简易的判断谁当U,谁当V的办法是比较困难的。
学生已经判断出U和V了,但是接下来的积分过程比较慢,想要个快速展开分部积分表达式的方法。
首先:我们要想清楚的是,分部积分应用在哪些场景呢? 换句话说,在什么情况下,我们会考虑到使用分部积分?
主要有两个原因:
1、被积函数表达式出现了不同类型函数的乘积;
2、在1的基础上,求udv的积分困难,但是求vdu的积分好求时。
基于以上两点,我们的数学系前辈们发明了分部积分。
我们先弄明白了分部积分的诞生来源,接下来需要考虑的是,考试真题或者说平时做题过程中,都会遇到哪些类型的函数进行相乘呢?
如何快速判断出U和V?

这个U和V就好像是两个人一起干活,一个干求导,一个干积分,现在的目标是积分求出他们两乘积的原函数,你是主人,要协调好这两个人,选出那个易于求导的U和还易于积分的V,让他们干自己容易干的活。诺,你看,现在的情况是出现了dv(对V求导)困难了,而对U求导比较简单(du),因此才出现了分部积分公式。
就拿上面的3个类型进行说明吧!
比如对于种类型,多项式和其他类型相乘时,我们选谁当做U呢?当然是选择求导简单的当做U了,而多项式和三角函数、指数函数相乘时,很明显对于多项式更容易求导,因此我们选择多项式做为U。
对于第二种类型,指数函数和三角函数相乘,这两个求导和积分都差不多,选这个当做U或者当做V,都不是什么困难的事,这就是口诀为什么有 “反对幂三指”和“反对幂指三” 两个版本的原因。
对于第三种类型,多项式和对数或者反三角在一块,你这时候就要留意了,因为对于多项式来讲,对它求导或者积分都不是什么困难的事,但是对于反三角函数来说,对它求积分好像确实是有点困难,反倒是对反三角求导比较简单一些。因此,在类型3中,我们往往将对数和反三角函数作为U。
总结一下:当我们碰到一个被积函数为两个不同类型的相乘时,下意识要使用分部积分了,此时你可以不用背口诀,你就简单的想,我让谁去求导且剩下的那个人干积分还不是很困难,那我就选谁当做U。
如何快速展开分部积分表达式?

可以看出,这个表格的行是写容易求导的人,对U不断地求导,第二行是写容易积分的人,对V不断地做积分,那么,根据表如何写出下来的表达式呢?
口诀就是:“以U为起点,左上右下,错位相乘,正负相间,最后一项写积分”。
有同学会问:我求导到啥时候?正负号如何规定的?用这个表怎么写展开式呢?
对于本题来讲,行要对多项式求导至0,正负号是这样规定的,规定项为正,接下来是负号,就这样按顺序写就行。表格的最后一项是积分,被积函数是U的最后一项和V的最后一项的乘积。按顺序写完后,依次写下去整理即可。
再看第二个例子:

由于三角函数在求两次导后,会出现原型,因此,这类一般行“求导至循环”。
最后,再来第三个例子:

对于反三角函数或者对数函数做U求导,一般只求一次导,即求导至反三角符号和对数符号消失为止。
通过以上3个例子的介绍,相信大家对这个分部积分的推广公式如何使用应该有了一定的印象。
总结一下:对于两个不同的函数乘在一起做积分,我们就要权衡好谁来求导简单一些,谁做积分更容易一些,然后用分部积分的推广公式来展开。
大家可以不用死记硬背分部积分那么长的推广公式,你就记住一点:我对行求导,对第二行做相应的积分,求导到什么程度呢?多项式一般是求导到0,三角函数一般是求导至循环,反三角和对数是求导至符号消失,最后利用口诀:“以U为起点,左上右下,错位相乘,正负相间,最后一项写积分”的原则,就可以快速、正确的写出分部积分的表达式!
想要了解更多关于A-level科目学习技巧等信息,可以扫码关注锦秋A-level,锦秋A-Level项目针对不同学员、不同层次的学习需求,有针对性的制定课程计划和教学方式,同时配备海量国际背景的教师和专业助教团队,双管齐下。专业的语言培训、完善的考试服务、高端的留学申请,贯彻“一站直达”的服务理念,只为帮学生梦圆,斩获英国G5!

| 大学名称 | QS排名 |
|---|