
在A-Levels纯数学的知识结构中,数列(sequence and series)是一个常见的知识点,首先,在学习之前,我们要明确数列的基本概念。数列(sequence/progression)是由若干个数(可能是有限个,也可能有无穷多个)线性排列而成的集合。比如1,3,5,7,9…
定义或者表示一个数列通常有三种方式。
直接列举
例1:1,3,5,7,9;
例2:u1=1,u2=3,u3=5,u4=7,u5=9。
例3:
n (position)12345
un (value)13579
通项公式general formula
如果un可以用n的表达式写出,则这个表达式称为数列的通项公式。利用通项公式,我们就可以根据项的位置,求出项的值。
例4:
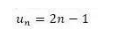
递推公式recursive formula/recurrence relation
如果数列的相邻项(un和un+1)之间有某种有规律的联系,可以用递推式来定义数列。
例5:一个数列用以下两个式子定义,

不难看出,上述例4-5定义的数列是等价的,并且它们的前5项和例1-3是相同的。
数列的前n项和(the sum of the first n terms)
很多时候,我们不仅关心数列的第n项(the nth term, un)是什么,还关心数列的前n项和(the sum of the first n terms)。
前n项和,通常记为Sn,定义为
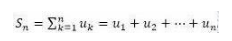
最常见的两种数列
等差数列(arithmetic sequence)
等差数列理解起来很简单,数列中后一项减去前一项的差值是相等的,这样的一列数就是等差数列。相邻两项的差为常数的数列称为等差数列,这个常数称为公差(common difference)。比如1,3,5,7,
就是个等差数列,它的公差为2。
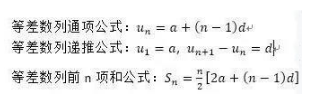
等比数列(geometric sequence)
我们用a表示等差数列的首项,r表示公差,则有

我们直接给出结论
数列是从自然数集(set of natural number)到任意数集的映射(函数),也就是说,它的实质就是定义域(domain)为自然数的函数。
等差数列对应于一次函数(linear function)
等比数列对应于指数函数(exponentials)
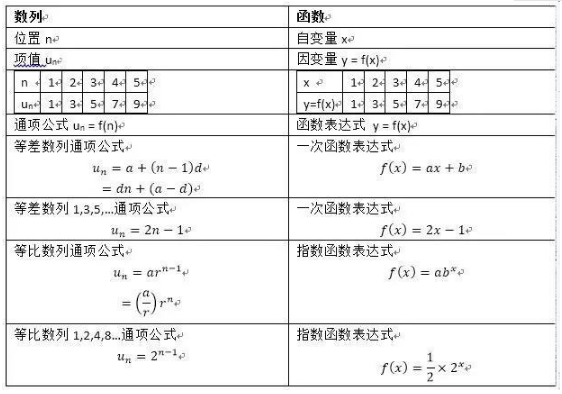
等比数列的定义也是很简单,后一项比上前一项的值是相等的,这个比值叫做公比。相邻两项的比为常数(不能为0)的数列称为等比数列,这个常数称为公比(common ratio)。锦秋A-Level项目针对不同学员的不同层次的学习需求,设置一站式计划、G5学霸计划和国际班互补计划三大课程体系,并且有针对性的制定课程计划和教学方式,开设的课程有数学、进阶数学、物理、化学、生物、经济学、会计学等,紧抓中国学生理科优势,进行课程组合化,请关注锦秋A-Level官网资讯,下方为我们的官方微信号:(微信号: xhdjinqiu)

| 大学名称 | QS排名 |
|---|